What Are Source Address Blacklists? There are two common
practices in formulating a blacklist. Sites such as DShield.org compile
global worst offender lists (GWOL) of the most prolific attack
sources, and regularly post firewall parsable filters of these lists to
help the Internet community fight back. Another common practice is for
a local network to create its own local worst offender list
(LWOL) of those sites that have attacked it the most. LWOLs have the
property of capturing repeat offenders that are indeed more likely to
return to the local site in the future but are only reactive to
new encounters with previously unseen attackers. On the other hand,
while GWOL has the potential to inform a local network of highly
prolific attackers, it also has the potential to provide a subscriber
with a list of addresses that will simply never be encountered.
Highly Predictive Blacklists (HPBs) represent a radically different
approach to blacklist formulation. HPB are derived uniquely per DShield
contributor, and rank the attack sources using an estimation
of the source's probability to attack that contributor in the
future. The HPB algorithm exploits a correlation relationship that was
originally observed in
Katti
et. al.. It was found that within the DShield repository, there
are groups of networks that share various degress of common
attacker overlap. We call networks that share significant attacker overlap
correlated victims. In formulating HPB for a network "A", we treat attack sources
that have reportedly made attacks on networks correlated with "A" differently
from attack sources that attacked the same number but uncorrelated networks.
The former are more probable to attack "A" and should be included in
A's HPB with high priority. (Traditional blacklisting approaches such as GWOL
treat these two attackers equally, therefore, ignore the characteristics of
individual networks shown in the alert history.)
The Key Idea of HPB is to
use peer-based correlations to estimate
attack probabilities of that an attack source poses to each
contributor. We model the correlation relationship
between networks as a graph (We call it correlation graph). The probability distribution is simulated
by a random walk on the correlation graph: A source walks on the
correlation graph, going from one node to another by following the
correlations among the victim networks. The source chooses an edge to
follow with a probability proportional to the strength of correlation
between the two victims connected by the edge. The stable distribution
of the random walk provides estimation on the source's probability of
attacking each network in the graph. (Similar types of random walk have
been applied in other probability propagation and estimation systems,
such as Google's PageRank.)
>
Suppose we have a collection of past attacks made by a set of
sources. An example is given in Table 1.
Table 1:
Attack Table
| |
v1 |
v2 |
v3 |
v4 |
v5 |
| s1 |
X |
X |
|
|
|
| s2 |
|
X |
|
|
|
| s3 |
X |
X |
|
X |
|
| s4 |
|
X |
X |
|
|
| s5 |
|
|
X |
|
|
| s6 |
|
|
X |
X |
|
| s7 |
|
|
|
|
X |
|
The rows represent attack sources and the column represent
the targeted networks (attack victims). An ``X'' in the table cell
indicates that the corresponding source has reportedly attacked the
corresponding network. Consider s2 and s7.
Although they have attacked the same number of victims, from the
viewpoint of v1, one may say that s2
is more likely to attack than s7, because s2
has attacked v2, which shares more common attackers
with v1. Now compare the source s5
to s7. Both sources attacked only one network. None
of these networks share common attacks with v1.
However, for v1, s5 and s7
are not equal. Notice that v2 shares common attacks
with v1, and v3 shares common
attacks with v2. A path v3 – v2 – v1
connects s5
to v1. One may say that s5 is
more likely to attack for v1.
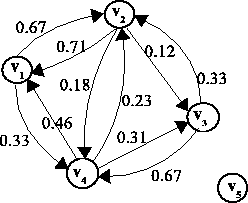Figure 1:Correlation Graph
We model the attack correlation as a graph.
The correlation graph is a weighted
directed graph G = (V, E). The nodes in the
graph are the victims, i.e. V = {v1, v2, ...}
There is an edge from node vi
to node vj if vi is correlated
with vj. The weight on the edge is proportional to
the strength of this correlation. Figure 1
shows the correlation graph for the victims in Table 1.
We rank an attack source, with respect to a victim, using the source's
probability to attack the victim. We estimate this probabilities in the
following way: suppose we have an estimation on source s's
probability of attacking victim vi. Following the
outgoing edges of vi, A fraction of this probability
can be distributed to the neighbors of vi in the
graph. Each neighbor receives a share of this probability that is
proportional to its strength of correlation with vi
(i.e., proportional to the weight of the edge from vi
to that neighbor.) Suppose vj is one of these
neighbors in the correlation graph. A fraction of the probability
received by vj is then further distributed, in the
similar fashion, to its neighbors. The propagation of probability
continues until the estimations for each victim reach a stable state.
Such a probability-propagation process can be simulated by a random
walk on the correlation graph.
Let Ps(v) be the estimate of the total
probability that s attacks v. Let Wij
be the correlation strength from victim vj to vi
and Bs(vi) be an initial
estimation based on whether s attacks vi in
the attack table. The stable distribution of the random walk is the following:
The full HPB system implements many other practical considerations for
blacklisting. However the source ranking and the probability estimation
by random walk are the heart of the system. Our experiments show that
the HPB exhibits a higher hit count than traditional blacklists for
most of the contributors. The experiments also show that HPB's performance is
consistent over time,
and these advantages remain stable across various list lengths and
predict windows.
